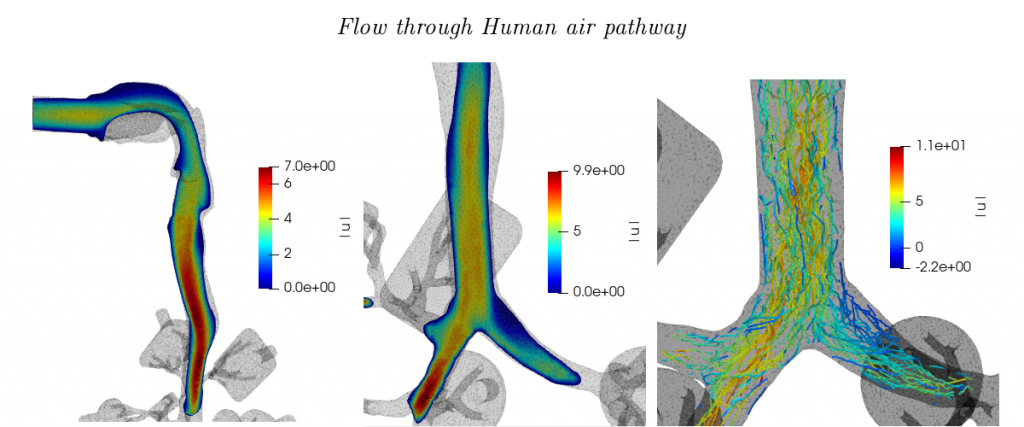
Particle deposition on human air pathway using Turbulence Modelling
Authors: Thivin Anandh, Lokesh M, Prof. Sashikumaar Ganesan
This project involves modelling of the turbulent fluid flow in the human air pathway geometry using Turbulence modelling methods and then coupling them with the Lagrangian approach of tracking particles in that fluid flow to identify the deposition patterns (fractions) in within the geometry.
Arbitrary Lagrangian Eulerian (ALE) framework using In compressible Navier Stokes Equations for Moving Domain Problems
Authors: Thivin Anandh, Prof. Sashikumaar Ganesan
AI Augmented large scale simulation of wind farms using PINNS & ROM
Authors: Thivin Anandh, Divij Ghose, Protyush, Rajarshi
AI FOR DEFENCE
Authors: Lokesh Mohanty, Protyush Pradyut Chowdhury, Prof. Sashikumaar Ganesan